<<<На главную
Moritz Maab
Suffix
Trees and their Applications
Суффиксные деревья и их приложения
перевод глав, содержащих
основные определения
и алгоритмы построения
суффиксных деревьев
Перевод: Погорский Н.В.
2004
Суффиксные звенья и двойственные суффиксные
деревья
Требования суффиксного дерева к памяти
Алгоритм mcc (McCreight`s
Algorithm)
Алгоритм Укконена (Ukkonen’s Algorithm)
Интерактивное (on-line) конструирование
атомарного суффиксного дерева
От алгоритма ast к ukk: интерактивное
(on-line) построение компактного суффиксного дерева
Связь между алгоритмами ukk и mcc
Шаги алгоритма mcc для слова ababc
Шаги алгоритма ukk для слова ababc
Структура данных
Основные
определения
Пусть S – непустое множество
символов, называемое алфавитом. Последовательность символов (возможно пустая)
из алфавита обозначается буквами r,
s и t. t-1 обозначает
перевернутую строку. Отдельные символы обозначаются буквами x, y
или z. e –
пустая строка. Символами из алфавита являются буквы a,b,
… .
Пока размер алфавита принимается постоянным.
Пусть |t|
обозначает длину строки t.
Пусть Sm – все строки длины m, S* = ![]() и S+ = S* \ {e}.
и S+ = S* \ {e}.
Префикс w строки t – строка такая, что wv = t
для некоторой (возможно пустой) строки v. Префикс называется правильным, если |v| не ноль.
Суффикс w строки t – строка такая, что vw = t
для некоторой (возможно пустой) строки v. Суффикс называется правильным, если |v| не ноль.
Подстрока w строки t называется правым ветвлением, если t может быть
представлено как uwxv и u`wyv` для некоторых строк u, v, u` и v`, и букв x
¹ y. Левое ветвление определяется аналогично.
Определение. (S+-дерево) S+-дерево T – корневое дерево с ребрами,
помеченными из S+. Для каждого символа a из алфавита, каждый узел в
дереве T имеет самое большее одно ребро метка которого начинается c символа a. Реберо от
t до s с меткой v мы будем обозначать t ®v s.
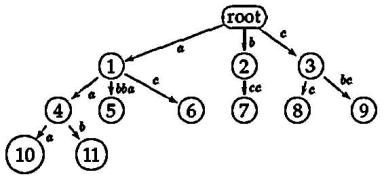
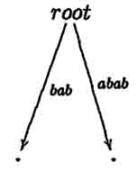
S+-дерево
Если T является S+-деревом с узлом k тогда path(k) – строка которая представляет собой конкатенацию всех
меток ребер от корня до k. Мы назовем w местоположением w, для которого path(w) = w.
Т.к. каждая ветвь уникальна, если path(t) = w мы можем обозначить узел t за w. Поддерево узла w
обозначается Tw.
Слова которые представлены в S+-дереве T даются множеством words(T). Слово w входит во
множество words(T) тогда и только тогда, когда существует v, такое,
что wv – узел дерева T.
Если строка w входит в words(T), w = uv, u – узел дерева T, пару (u, v) будем называть
ссылочной парой w по отношению к дереву T. Если u – наидлиннейший префикс, такой,
что (u, v) – ссылочная пара, мы будем называть (u, v)
канонической ссылочной парой. Тогда мы будем писать w = (u,v).
В нашем примере (e, ab) – ссылочная пара для ab
и ab = (1,b) –
каноническая ссылочная пара.
Местоположение w = (u,v) называется явным, если |v| = 0 и неявным в противном
случае.
Определение. (Атомарное и Компактное S+-дерево) S+-дерево T, в котором каждое ребро
помечено одиночным символом называется атомарным (каждое местоположение явно).
S+-дерево T, в котором каждый узел является либо корнем, либо листом
или узлом ветвления называется компактным.
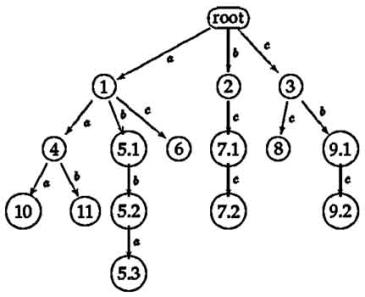
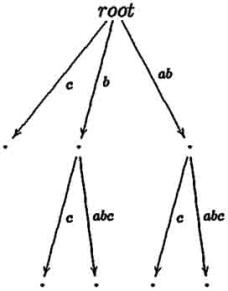
Атомарное дерево
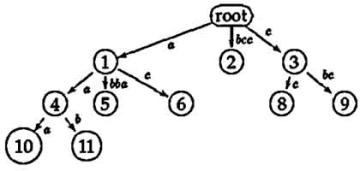
Компактное дерево
Атомарное S+-дерево также называют “trie” (луч). Атомарное и компактное S+-дерево уникально определены
словами, которые они содержат.
Определение. (Суффиксное дерево) Суффиксное дерево для строки t – это S+-дерево такое, что words(T) = {w| w – подслово
t}. Для строки t атомарное суффиксное дерево обозначается ast(t),
компактное суффиксное дерево обозначается cst(t).
Обратное префиксное дерево строки t – это суффиксное дерево для
строки t-1.
Вложенный суффикс – суффикс, который появляется в
слове t
где-нибудь ещё, наидлиннейший вложенный суффикс называется активным суффиксом строки t.
Лемма(1). (О
явных местоположениях в компактном суффиксном дереве) Местоположение w явно в компактном суффиксном
дереве тогда и только тогда, когда:
- w
– не является вложенным суффиксом t или
- w
– правое ветвление.
Доказательство. “à”:
Если w –
явно, то это может быть либо лист, либо вершина ветвления или корень (в этом
случае w = e и w – вложенный суффикс t).
Если w – лист, тогда также является и суффиксом t. Значит это должен быть не вложенный суффикс, т.к. иначе, он появился бы где-нибудь еще в строке t: $v – суффикс t такой, что w – префикс v. Этот узел не может быть листом.
Если w – узел ветвления, тогда должны
существовать по меньшей мере два выходящих ребра из w с различными метками. Это означает,
что существуют два различных суффикса u, v, что w – префикс u и w – префикс v, где v = wxs, u = wx’s’, x ¹ x’. Следовательно, w – правое ветвление.
“ß”:
Если w не
является вложенным суффиксом t, это
должен быть лист. Если w –
правое ветвление, то имеются два суффикса u и v, u = wxs, v = wx’s’, x ¹ x’, тогда w является узлом ветвления. ÿ
Теперь легко видеть, почему ответ
на вопрос входит ли слово w в
строку t
может быть найден за время O(|w|), т.к. нужно только проверить
является ли w
местоположением (явным или неявным) в cst(t).
Метки ребер должны представлять
собой указатели на положение в строке, чтобы суффиксное дерево расходовало
память размером O(n). Метка (p,q) ребра означает подстроку tp..tp или пустую строку, если p > q.
Укконен вводит название открытые ребра для ребер, заканчивающихся в листьях.
Пометки открытых ребер записывают как (p, ¥) вместо (p, |t|), где ¥ – всегда длина большая, чем |t|.
Определение.
(Суффиксное звено) Пусть T – S+-дерево. Пусть aw –
узел T, v – наидлиннейший суффикс w такой, что v –
также узел T. Непомеченное ребро от aw до v называется суффиксным звеном.
Если v = w оно называется атомарным.
Утверждение(1). В ast(t) и ast(t$), где $ Ï t, все суффиксные звенья являются
атомарными.
Доказательство.
Символ $ называется символом-стражем.
Первая часть следует из определения, т.к. местоположения являются явными. Для
доказательства второй части мы должны показать, что для каждого узла aw, w также
является узлом cst(t). Если aw – узел cst(t), то является либо листом, либо узлом
ветвления. Если является листом, тогда w – не вложенный суффикс t. Благодаря символу-стражу, из
леммы (1) следует, что все суффиксы (включая корень, пустой суффикс) являются
явными, т.к. только корень – вложенный суффикс. Поэтому w является листом или корнем. Если
aw –
узел ветвления, тогда aw –
правое ветвление, как и w.
Следовательно, местоположение w –
явно по лемме (1). ÿ
Как следует из этого доказательства, символ-страж
гарантирует существование листьев для всех суффиксов. С таким символом не может
быть вложенных суффиксов, кроме пустого. Если мы опустим символ-страж,
некоторые суффиксы могут стать вложенными и их местоположения станут неявными.
Суффиксные
звенья и двойственные суффиксные деревья
Рассмотрим дерево T-1. Оно имеет узел w-1 для каждого узла w дерева
T и ребро от w-1 до (vw)-1 для каждого суффиксного звена
от vw до w в дереве T.
Утверждение(2). T-1 является S+-деревом.
Доказательство. От противного: предположим, что есть узел w-1 в дереве суффиксных звеньев,
имеющий два a-ребра. Тогда должны быть два суффиксных звена в суффиксном
дереве T от uaw до w и от vaw до w. Здесь u ¹
e и v ¹ e потому, что, если aw явно,
суффиксное звено будет указывать туда вместо w.
Если uaw или vaw – внутренние узлы, тогда uaw или vaw – правые
ветвления в T. Но тогда слово aw должно быть также правым ветвлением и является явным
местоположением, что является противоречием.
Если uaw или vaw – листья, uaw или vaw должны
быть суффиксами t и тогда uaw – суффикс vaw или vaw – суффикс uaw, в этом случае суффиксное звено от vaw
должно указывать на uaw или наоборот. ÿ
Проходя суффиксные звенья последовательно от w до корня, получаем путь, представляющий подслово строки t-1.
Утверждение (3). (ast(t))-1 = ast(t-1).
Доказательство. Все суффиксные звенья дерева ast(t) атомарные по утверждению (1). Тогда можно провести простой вывод:
w-1 ®a (aw)-1 – ребро в (ast(t))-1 тогда и только тогда, когда aw ®a w – суффиксное звено в ast(t) ó имеются узлы aw и w в ast(t) ó в ast(t-1) присутствуют узлы aw-1 и w-1 в ó в ast(t-1) существует ребро w-1 ®a (aw)-1. ÿ
Для компактного суффиксного дерева имеется более слабая двойственность.
Утверждение (4). ((cst(t))-1) -1 = cst(t).
Без доказательства.
Дальнейшее изучение этой двойственности ведет к понятию дерева аффиксов.
Требования
суффиксного дерева к памяти
Утверждение (5). Компактное суффиксное дерево может быть представлено в виде, требующем O(n) памяти.
Доказательство. Суффиксное дерево содержит самое большее один лист на каждый суффикс (в точности один с символом-стражем). Каждый внутренний узел должен быть узлом ветвления, следовательно, внутренний узел имеет, по меньшей мере, двух потомков. Каждое ветвление увеличивает число листьев самое меньшее на единицу, поэтому мы имеем не более n внутренних узлов и не более n листьев.
Для представления строк, являющихся метками ребер, мы используем индексацию в исходной строке, как описано выше. Каждый узел имеет не более одного предка и, таким образом, общее число ребер не превышает 2n.
Аналогично, каждый узел имеет не более одного суффиксного звена, тогда общее число суффиксных звеньев также ограничено числом 2n. ÿ
Как пример суффиксного дерева с 2n – 1 вершинами можно рассмотреть дерево для an$.
Размер атомарного суффиксного дерева для строки t составляет O(n2).
Алгоритм mcc (McCreight`s Algorithm)
Основная
идея
mcc начинает работу с пустого дерева и добавляет суффиксы начиная с самого длинного. (Поэтому mcc не является on-line алгоритмом, т.е. для его работы необходима вся строка целиком). mcc требует, чтобы строка завершалась специальным символом, отличным от других, так, чтобы ни один суффикс не являлся префиксом другого суффикса. Каждому суффиксу в дереве будет соответствовать лист.
Для алгоритма мы определим sufi – текущий суффикс (на шаге i), headi (головаi) – наибольший префикс суффикса sufi, который является также префиксом другого суффикса sufj, где j < i. taili (ховстi) определим как sufi – headi.
Ключевой идеей алгоритма mcc является соотношение между headi и headi-1:
Лемма(2). Если headi-1 = aw где a – буква алфавита, w – строка (может быть пустая), тогда w - префикс headi.
Доказательство. Пусть headi-1 = aw. Тогда существует j, j < I, такой, что aw является как префиксом sufi-1, так и префиксом sufj-1. Тогда w – префикс sufj и sufi, следовательно, w является префиксом головы w headi. ÿ
Мы знаем местоположение headi-1 = aw, и если мы будем иметь суффиксное звено, то можем быстро перейти к местоположению w – префикса головы headi без необходимости находить путь от корня дерева. Но местоположение w могло бы не являться явным (если местоположение headi-1 не было явным на предыдущем шаге) и суффиксное звено могло бы быть ещё не установлено для узла headi-1.
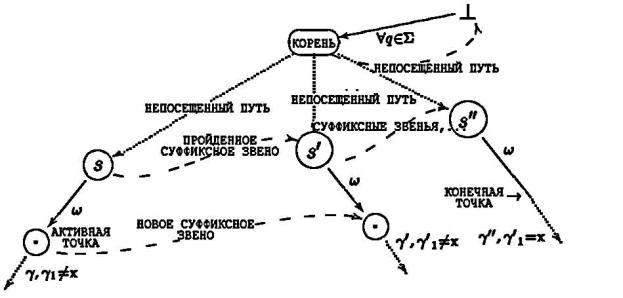
Решение, данное McCreight, находит узел headi за два шага: “повторное сканирование” (“rescanning”) и “сканирование” (“scanning”). Мы только проходим дерево от узла headi-1 пока не найдем суффиксное звено, следуем по нему и затем применяем повторное сканирование пути до местоположения w (которое является простым, потому что мы знаем длину w и это местоположение существует, так что мы не должны читать полные метки ребер, двигаясь вниз по дереву, мы можем просто проверять только начальные буквы и длину слов).
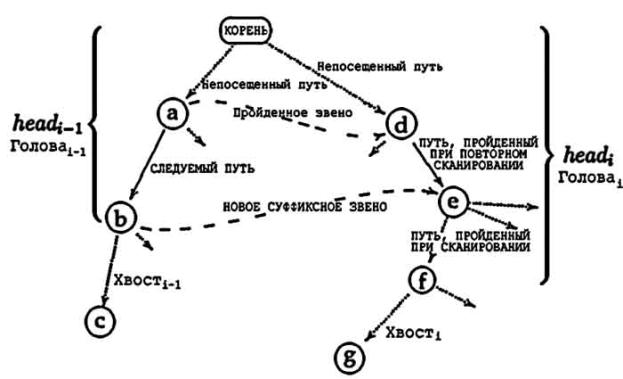
Рисунок демонстрирует эту идею. Вместо попытки найти путь от корня до узла f, алгоритм переходит до a, следует суффиксному звену до d, проводит повторное сканирование пути до (возможно неявного) местоположения e и остается найти путь до f, проходя посимвольно.
Алгоритм
Алгоритм состоит из трех частей.
(1)Сперва он определяет структуру предыдущей головы (old header), находит следующее
доступное суффиксное звено и следует по нему. (2)Затем он повторно сканирует
часть предыдущей головы, для которой длина является известной (эта часть
названа b). (3)Наконец алгоритм
устанавливает суффиксное звено для headi-1, сканирует оставшуюся часть headi (названную g) и добавляет новый лист для taili(хвостi). Узел ветвления создается во второй
фазе повторного сканирования, если не существует местоположения w. В этом
случае сканирование не является необходимым, потому что если headi была бы длиннее чем ab, abg являлось бы правым ветвлением
(подстрока w строки t называется правым ветвлением, если t может быть представлено как uwxv и u`wyv` для
некоторых строк u, v, u` и v`, и букв x ¹ y) но по
лемме (2) ab является также правым
ветвлением, так узел ab уже должен существовать. Узел создается в третьей фазе если местоположение headi ещё не явно.
Алгоритм mcc
Вход: строка t
1
T := пустое_дерево;
2
Head0 := e;
3
n := length(t);
4
for i = 1 to n do
5
найти
c, a, b такие,
что
a.
headi-1 = cab,
b.
если
предок узла headi-1 не корень, тогда это ca, в противном случае |a| = 0,
c. |c| £ 1 и (|c| = 0 « |headi-1| = 0)
6 if ( |a| > 0) then
7 следовать по суффиксному звену от узла ca до a;
8
end
if
9
ab := Rescan(a, b);
10 установить суффиксное звено от headi-1 до ab;
11
(headi, taili) := Scan(ab, sufi
- ab);
12 добавить лист соответствующий taili;
13 end for
Обратите внимание, что если |a| = 0
тогда a = корень и узнается одинаково быстро, как следуя
суффиксному звену согласно строке 7 алгоритма.
Процедура Rescan ищет местоположение ab. Если местоположение ab еще не задано, добавляется новый
узел. Этот случай имеет место, когда голова (head) просмотрена целиком: если
голова (head) длиннее (и узел уже определен), ab должно
являться префиксом более чем двух суффиксов и также является левым ветвлением t (подстрока
w строки t называется левым ветвлением, если t может быть представлено как uxwv и u`ywv` для
некоторых строк u, v, u` и v`, и букв x ¹ y).
Местоположение ab может являться только явным,
если этот узел уже является узлом ветвления, и если ab не было левым ветвлением тогда headi-1, должно быть, был длиннее,
потому что встретился более длинный префикс.
Procedure
Rescan(n, b)
Вход: узел n, строка b
1
l := 1;
2
while l £ |b| do
3
найти ребро e = n ®w n', w1 = bl;
4
if l + |w|
> |b| + 1 then
5
k := |b| – l + 1;
6
расщепить
ребро e с новым узлом m и ребрами n ®w[1]…w[k] m и m ®w[k+1]…w[|w|] n';
7
return m;
8
end if
9
l := l + |w|;
10
n: = n’;
11 end while
12
return n’;
Процедура Scan ищет в глубину дерева и
возвращает позицию.
Procedure Scan(n, g)
Вход: узел n, строка g
1
l := 1;
2
while существует ребро e
= n ®w n', w1 = gl do
3
k := 1;
4
while wk = gl и k £ |w| do
5
k := k + 1;
6
l := l + 1;
7
end while
8
if k > |w| then
9
n := n’;
10
else
11
расщепить ребро e с новым узлом m и ребрами n
®w[1]…w[k-1] m и m ®w[k]…w[|w|] n';
12
return (m, gl…g|g|);
13
end if
14 end while
15 return (n, gl…g|g|);
Сложность
алгоритма mcc
Утверждение. Сложность алгоритма mcc по времени составляет O(n).
Доказательство. Пусть t – основная строка и n = |t|. Основной цикл алгоритма mcc
выполняется за время n, каждый шаг цикла затрачивает константное время, если не брать
в расчет вызовы процедур Scan и Rescan.
Rescan затрачивает время,
пропорциональное числу посещенных узлов inti.
Сканирование имеет место в суффиксе resi текущего суффикса sufi (resi = sufi - a). Т.к. каждый узел, с которым сталкиваются при повторном сканировании,
имеет суффиксное звено, будет иметься
непустая строка w (пометка ребра), которая содержится в resi, но не содержится в resi+1 для каждого узла. Поэтому resi ³ resi+1 + inti. Следовательно
![]()
и все вызовы процедуры Rescan занимают время O(n).
Процедура Scan не может просто перескакивать от узла к узлу, но символы
между просматриваются друг за другом. Пусть g(i) = headi - a(i)b(i). Тогда |g(i)| - число просматриваемых символов. По определению a
и b
|headi-1|
= |headi| + |g| – 1. Следовательно, общее число просмотренных символов во всех
вызовах процедуры Scan составляет
![]() . ÿ
. ÿ
Алгоритм Укконена (Ukkonen’s Algorithm)
Укконен разработал свой линейный алгоритм исходя из другой (и
более интуитивно понятной) идеи. Он работал над автоматами соответствия строк и
его алгоритм получен из одной конструкции атомарного суффиксного дерева (в
некоторой литературе называемой “trie”). Сначала вкратце опишем тот алгоритм, а затем получим
алгоритм Укконена.
Интерактивное
(on-line)
конструирование атомарного суффиксного дерева
Как показано, атомарное суффиксное дерево имеет размер O(n2). Поэтому любой алгоритм
требует по крайней мере этого времени для построения атомарного суффиксного
дерева. Следующий алгоритм удлиняет суффиксы на единицу на каждом шаге. Каждое
промежуточное дерево после i-го шага является атомарным суффиксным деревом для слова t1…ti. Алгоритм начинает вставлять
новые листья соответствующие самому длинному
суффиксу и следует суффиксным звеньям до более коротких суффиксов, пока
не достигает узла, в котором соответствующие ребра уже существуют. Гарантирует
завершение этого цикла дополнительный узел ^, отличный
от всех символов алфавита. Мы имеем суффиксное звено от корня до ^ и помеченное как x ребро от ^ до корня для каждого x из
алфавита.
Алгоритм ast
Вход: строка t
1
T := пустое_дерево;
2
Добавить
корень и ^ в дерево;
3
for (всех x из алфавита S) do
4
добавить
ребро (^ ®x корень);
5
end for
6
суффиксное_звено(корень)
:= ^;
7
n := длина(t);
8
наидлиннейший_суфикс
:= корень;
9
предыдущий_узел
:= корень;
10 for i := 1 to n do
11
текущий_узел
:= наидлиннейший_суфикс;
12
while (не существует ребра e = (текущий_узел ®ti временный_узел)) do
13
добавить
ребро (текущий_узел ®ti новый_узел) с новым узлом;
14
if (текущий_узел = наидлиннейший_суфикс) then
15
наидлиннейший_суфикс
:= новый_узел;
16
else
17
суффиксное_звено(предыдущий_узел)
:= новый_узел;
18
end if
19
предыдущий_узел
:= новый_узел;
20
текущий_узел
:= суффиксное_звено(текущий_узел);
21
end while
22
суффиксное_звено(предыдущий_узел)
:= временный_узел;
23
end for
От
алгоритма ast к ukk:
интерактивное (on-line)
построение компактного суффиксного дерева
Данный выше алгоритм теперь будет
преобразован в линейный алгоритм построения компактного суффиксного дерева. На
шаге i + 1
алгоритм ast добавляет
новые узлы в граничный путь (boundary path). Граничный путь (boundary path) –
путь от наидлиннейшего суффикса по суффиксным звеньям до помеченного меткой ti+1
ребра. Пусть sj –
подслово tj…ti слова t, sj – местоположение соответствующего
узла в дереве ast(sufi) с корнем si+1 и si+2 = ^. Пусть l – самый большой индекс, такой, что для
всех узлов sj, j < l, узел и ребро добавлены. Теперь, пусть
k –
наибольший индекс, такой, что для всех узлов sj (j < k) sj является
листом. После шага i
наидлиннейший суффикс sufi = s1
является листом и ^ = si+2
всегда имеет помеченное как ti
ребро, так что очевидно 1 < k £ l < i+2 на шаге i + 1.
Назовем sk активной точкой (active point) и sk – конечной точкой (endpoint). sk –
активный суффикс слова t1…ti, также являющийся наидлиннейшим
вложенным (вложенный суффикс – суффикс который появляется в слове t где-нибудь ещё, наидлиннейший
вложенный суффикс называется активным суффиксом t). Алгоритм ast вставляет два различных вида ti - ребра: пока активная точка
является листьями, которые расширяют ветвь, после этого каждое ребро начинает
новую ветвь. При применении этого к построению компактных суффиксных деревьев
одна ключевая идея Укконкна вводила понятие открытого ребра (открытые ребра – ребра идущие в листья дерева). При
этом ребра расширялись бы автоматически со строкой, и не было бы нужды
добавлять их вручную.
Теперь мы должны только описать,
как обновлять активную точку (первоначально – корень) и как добавлять узлы
ветвления и новые листья по граничному пути до конечной точки. Пусть Ti – компактное суффиксное дерево
после i-го
шага.
Лемма (3). Если
ссылочная пара (s, (k, i – 1)) – конечная точка для дерева Ti-1 на
шаге i,
тогда (s, (k, i)) – новая активная точка дерева Ti
на шаге i + 1.
Доказательство.
Пусть sj = (s, (k, i)). sj – активная точка дерева Ti, если sj – наидлиннейший вложенный
суффикс суффикса sufi,
если sj –
наидлиннейшее подслово суффикса sufi-1,
такое что sj –
окончание (на позиции s)
суффикса sufi,
если ti-ребро
из sj в
дереве Ti-1 и j – минимально, если sj – конечная точка Ti-1. ÿ
Т.к. текущая активная точка (и
другое позже достигнутое местоположение) могут быть неявными, алгоритм ukk
работает с ссылочными парами и добавляет узлы для создания явного местоположения
по мере необходимости. Когда, пройдя граничный путь, ukk
следует по суффиксному звену узла текущей ссылочной пары и затем делает канонической новую ссылочную
пару.
На каждого шага вызывается
процедура update,
которая добавляет все новые ветви для нового символа.
Procedure update(s, (k,i))
Вход: узел s, (s, (k,i)) – ссылочная пара для текущей
активной точки.
1
oldr :=
корень;
2
(b_конечная_точка,
r) :=
тест_и_расщепление(s, (k, i-1), ti);
3
while (не b_конечная_точка) do
4
добавить ребро r ®(i, ¥) m с новым узлом m;
5
if (oldr ¹ корень) then
6
суффиксное_звено(oldr) := r;
7
end if
8
oldr := r;
9
(s, l) :=
канонизация(суффиксное_звено(s), (k, i-1));
10
(b_конечная_точка,
к) := тест_и_расщепление(s, (k, i-1), ti);
11
end while
12
if (oldr ¹ корень) then
13
суффиксное_звено(oldr) := s;
14
end if
15
return (s, k);
Процедура тест_и_расщепление тестирует, является ли данное
(неявное или явное) местоположение конечной точкой, и возвращает это в первом
выходном параметре. Если не является конечной точкой, тогда добавляется узел (и
таким образом местоположение делается явным, если не было уже). Узел
возвращается как второй выходной параметр.
Procedure тест_и_расщепление(s, (k,p), x)
Вход: узел
s, (s, (k,p)) – каноническая ссылочная пара
которая тестируется, x – буква
которая проверяется как метка ребра.
1
if |tk… tp| > 0 then
2
пусть w =
(k’,p’) – метка ребра e = s ®w s’ с буквой w1 = tk;
3
if x = w[tk … tp] then
4
return (true, s)
5
else
6
расщепить e с новым узлом m и ребрами s ®wk’… wk’+|tk…tp|-1 m и s ®wk’+|tk…tp|…wp’ s’;
7
return (false,m);
8
endif
9
else
10
if (существует ребро s ®x… m) then
11
return (true, s);
12
else
13
return (false,s);
14
end if
15
end if
Процедура тест_и_расщепление ожидает каноническую ссылочную пару
для своей работы. Должно быть очевидно, что она требует константного времени
выполнения. Для получения канонической ссылочной пары мы имеем процедуру канонизация. Она возвращает только различные узлы
и различные стартовые индексы для меток ребер, так как конечный индекс должен
оставаться тот же самый.
Procedure канонизация(s, (k, p))
Вход: узел s, (s, (k, p)) – ссылочная пара подлежащая
канонизации.
1
if |tk… tp| = 0 then
2
return (s, k);
3
else
4
найти ребро e = s ®w s’ с w1 = t k;
5
while |w| £ |tk… tp| do
6
k := k + |w|;
7
s := s’;
8
if |tk… tp| > 0 then
9
найти ребро e = e = s ®w s’ с w1 = t k;
10
end if
11
end while
12
return (s, k);
13 end if
Теперь можно написать алгоритм
целиком.
Алгоритм ukk
Вход:
строка t
1
T :=
пустое_дерево;
2
добавить корень и ^ до T.
3
for
(всех букв x алфавита S) do
4
добавить ребро ^ ®x
корень;
5
end for
6
суффиксное_звено(корень) := ^;
7
n :=
длина(t);
8
s := корень;
9
k := 1;
10
for i := 1 to n do
11
(s,k) := канонизация(s, (k, i – 1));
12
(s,k) :=
update(s, (k, i));
13 end for
Как говорилось ранее, алгоритмы ukk и ast являются
интерактивными (on-line). Это свойство может быть
достигнуто, если мы заменим цикл (строка 10) на цикл, который останавливается,
когда нет новых символов на входе или найден завершающий символ.
Сложность
алгоритма ukk
Утверждение. Сложность алгоритма ukk по
времени составляет O(n).
Доказательство. Мы проанализируем время,
затрачиваемое процедурой канонизация и в
остальном независимо.
Для каждого шага алгоритма
процедура update вызывается однажды. Время выполнения было бы константным, если бы не
выполнения цикла while (и
процедуры канонизация, которую рассмотрим позже).
Пусть resi –
активная точка на шаге i. В
цикле while
процедура ukk
двигается по граничному пути от текущей активной точки до новой активной точки
(минус один символ), как доказано в лемме. Пусть w = resi. Для каждого перемещения в цикле
while,
берется суффиксное звено и w
уменьшается на единицу. В конце шага i (или
в начале шага i + 1)
w
увеличивается следующей буквой до формы resi+1.
Следовательно, число шагов в цикле while
составляет |resi| – |resi+1| +
1. Это дает сложность
![]()
Это также число вызовов процедуры
канонизация, так что мы будем рассматривать
цикл while
(строки 5 – 8 процедуры канонизация).
Процедура канонизация всегда вызывается для строки tk…ti-1. Эта
строка первоначально пуста и увеличивается с каждой итерацией алгоритма. На
каждой итерации цикла while при
выполнении процедуры канонизация
строка сокращается по крайней мере на один символ. Поэтому общее число итераций
может быть только O(n).
Вместе все части алгоритма дают
время O(n). ÿ
Связь
между алгоритмами ukk и mcc
Показано, что mcc и ukk
фактически исполняют те же самые абстрактные операции расщепления ребер и
добавление листьев в том же самом порядке. Они отличаются в управляющей
структуре и ukk
может быть преобразован в mcc. Это становится правдоподобным если обратить
внимание, что первый вставленный алгоритмом ukk лист является также самым длинным
суффиксом (станет самым длинным, когда строка вырастет до своего
заключительного размера), и что алгоритм ukk следует суффиксным звеньям тем же
самым способом, что и mcc, когда добавляется узел ветвления.
Также установлено, что это –
оптимизация управляющей структуры ukk, что
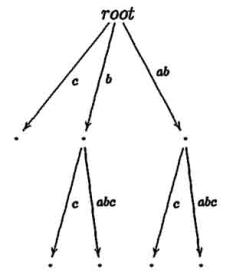
становится правдоподобным при взгляде на компактное суффиксное дерево cst(ababc). В то время как mcc
добавляет ветвь на каждой итерации, ukk не делает этого. В шагах 3 и 4 никакие ветви не добавляются, только
листья автоматически увеличиваются.
Примеры работы алгоритмов
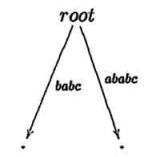
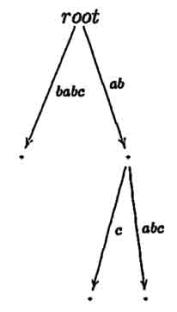
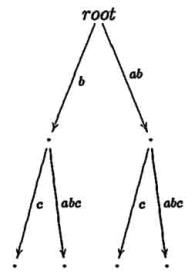
Шаги
алгоритма mcc для слова
ababc

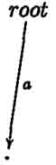
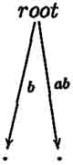
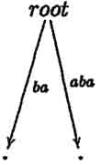
Шаги алгоритма ukk для слова
ababc
<<<На главную