<<<На главную
F. P. Preparata, M.I.
Shamos
Вычислительная геометрия
Разделы о региональном поиске
Содержание
1 Задача регионального поиска. Метод локусов
3 Метод прямого
доступа и его варианты
1 Задача регионального поиска. Метод локусов
Пусть
даны m точек на плоскости. Сколько из них лежит внутри заданного
прямоугольника, стороны которого параллельны осям координат? Очевидно, что
уникальный региональный запрос может быть обработан оптимально за линейное
время, так как надо только проверить каждую из m
точек, чтобы увидеть, удовлетворяет ли она неравенствам, задающим
прямоугольник. Аналогично необходима линейная затрата памяти, т.к. следует
запомнить только 2m координат. Нет никаких затрат на
предобработку, а время корректировки для новой точки равно константе. Какую
структуру данных можно использовать для ускорения обработки массовых запросов?
Следующее решение является примером использования метода локусов в
геометрических задачах: запросу ставится в соответствие точка в удобном для
поиска пространстве, а это пространство разбивается на области (локусы –
геометрические места точек), в пределах которых ответ не изменяется. Если
считать эквивалентными два запроса, на которые поступают одинаковые ответы, то
каждая область разбиения пространства поиска соответствует одному классу
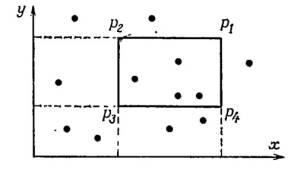
эквивалентности запросов. Удобно заменить запрос с прямоугольником четырьмя
подзадачами, по одной на каждую из его вершин, и совместить их решения для
получения окончательного ответа. В этом случае подзадача, связанная с вершиной p, состоит в определении числа точек Q(p) исходного множества, которые
удовлетворяют неравенствам x£x(p) и y£y(p),
т.е. числа точек в левом нижнем квадранте, определяемом вершиной p.
Говорят,
что точка (вектор) v доминирует над w, тогда и только тогда, когда для всех индексов i верно условие vi³wi. На
плоскости точка v доминирует над w тогда и только тогда, когда w
лежит в левом нижнем квадранте, определяемом v.
Итак Q(p) – число точек, над которыми
доминирует p. Число точек N(p1p2p3p4) в прямоугольнике p1p2p3p4 определяется следующим образом: N(p1p2p3p4) = Q(p1)-Q(p2)-Q(p4)+Q(p3).
Итак,
задача регионального поиска сведена к задаче обработки запросов о доминировании
для четырех точек. Свойство, облегчающее эти запросы, заключается в том, что на
плоскости существуют области удобной формы, внутри которых число доминирования Q является константой.
Предположим,
что из наших точек на оси x и y опущены перпендикуляры, а полученные линии продолжены в
бесконечность. Они создают решетку из (m+1)2
прямоугольников. Для всех точек p в любом из таких
прямоугольников Q(p)
– константа. Это означает, что доминантный поиск есть просто ответ на вопрос: в
какой ячейке прямоугольной решетки лежит заданная точка. После упорядочения
исходных точек по обеим координатам остается только выполнить два двоичных
поиска (по одному для каждой оси), чтобы найти ячейку, содержащую нашу точку.
Значит, время запроса будет равным только O(log m). К сожалению,
имеется O(m2) ячеек, поэтому нужна квадратичная память. Нужно, конечно,
вычислить число доминирования для каждой ячейки. Это можно легко проделать для
любой из ячеек за время O(m),
что приводит к общей затрате времени O(m3) на предобработку.
Затраты памяти и времени на предобработку слишком велики.
2 Многомерное двоичное дерево
Рассмотрим
более интересные и тонкие методы для задачи регионального поиска, которые
включают кроме подсчета осуществление выборки самих точек.
Начнем с простейшего примера регионального поиска – одномерного случая. Дано множество из N точек на оси x, запросным регионом является отрезок [x`,x``] (x-регион). Методом, дающим эффективный (оптимальный) региональный поиск, является двоичный поиск, то есть дихотомия искомого упорядоченного множества. Ясно, что x` – левый конец x-региона – локализуется на оси x дихотомией; на этом завершается поиск, а для осуществления выборки надо пройти ось x в направлении возрастания x вплоть до достижения правого конца x``. Структурой данных, обеспечивающей указанное действие, является прошитое двоичное дерево, листья которого дополнительно связаны в списке, отражающем порядок абсцисс; дерево и список обрабатываются на фазах соответственно поиска и выборки множества. Описанный метод оптимален как по времени запроса Q(log N + k), так и по памяти Q(N), где k – мощность выбираемого множества.
Естественно попытаться обобщить дихотомию на двумерный случай, где исходное множество является набором из N точек, лежащих на плоскости (x,y). То, что делается при дихотомии, есть не что иное, как последовательное разрезание региона на две части. В случае двух измерений всю плоскость можно считать бесконечным прямоугольником, который будет разрезан сначала на две полуплоскости прямой, параллельной одной из осей, скажем оси y. Затем каждая из этих полуплоскостей может разрезаться еще раз прямой, параллельной оси x, и т.д., меняя на каждом шаге направление разрезающей линии, например от x к y. Как выбирают разрезающие линии? В точном соответствии с тем же принципом, который используется при обычной дихотомии, т.е. руководствуясь принципом получения приблизительно равного числа элементов по каждую сторону от разреза. Мы пришли к обобщению дихотомии и к основной идее метода многомерного двоичного дерева [Bentley (1975)].
Назовем обобщенным прямоугольником
такую область на плоскости, которая определена декартовым произведением [x1,x2]x[y1,y2] x-интервала [x1,x2] и y-интервала [y1,y2], включая предельные
случаи x1 =
–¥, y1=–¥, x2=¥, y2=¥. Поэтому мы будем считать прямоугольником
также неограниченные полосы, любой квадрант или даже всю плоскость.
Процесс разбиения множества S путем разрезания плоскости лучше всего иллюстрировать в сочетании с построением двумерного двоичного дерева T. С каждой вершиной v дерева T мы неявно связываем прямоугольник R(v) и подмножество S(v) точек, лежащих внутри R(v); явно же, т.е. как фактические параметры этой структуры данных, свяжем с v одну избранную точку P(v) из S(v) и секущую прямую l(v), проходящую через P(v) и параллельную одной из координатных осей. Этот процесс начинается с определения корня T. С R(корень) соотносится вся плоскость, и полагается, что S(корень) = S; затем определяется точка pÎS, такая что x(p) – медиана множества абсцисс точек из S(корень), и полагается, что P(корень) = p, а с l(корень) соотносится прямая с уравнением x = x(p). Точка p разбивает S на два множества приблизительно равной мощности, назначенных потомкам корня. Процесс дробления прекращается, когда обнаружен прямоугольник, не содержащий внутри точек; соответствующий ему узел является листом дерева T.
Метод проиллюстрирован на примере с рисунком для множества из N = 11 точек.
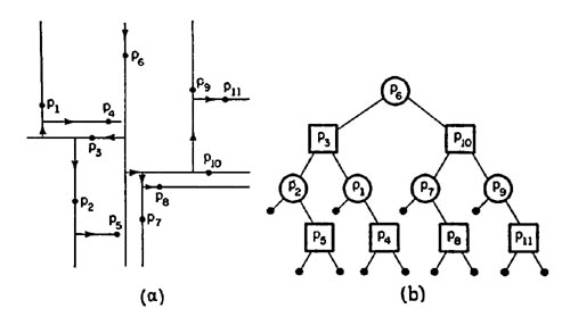
Узлы трех разных типов обозначены различными графическими символами: кружками – нелистовые узлы с вертикальной линией разреза, квадратами – нелистовые узлы с горизонтальной линией разреза, точками – листья. Такая структура данных часто называется 2-D-деревом.
Изучим использование структуры данных типа 2-D-дерева для регионального поиска. Алгоритмической схемой будет метод “разделяй и властвуй” в чистом виде. Действительно, рассмотрим взаимное расположение прямоугольной области R(v), связанной с вершиной v дерева T, и некоего прямоугольного региона D такого, что R(v) и D имеют непустое пересечение. Область R(v) разрезана на два прямоугольника R1 и R2 прямой l(v), проходящей через P(v). Если DÇR(v) полностью содержится в Ri (i = 1,2), то поиск продолжается с единственной парой типа (область, регион), а именно с (Ri,D). Если же область DÇR(v) разделена прямой l(v), то l(v) имеет непустое пересечение с D, а значит, D может содержать P(v). Поэтому сначала проверим, находится ли P(v) внутри D, и если да, то поместим эту точку в выбираемое множество; затем продолжим поиск с двумя парами типа (область, регион), а именно с (R1,D) и (R2,D). Этот процесс поиска прекращается при достижении любого листа.
Более строго любая вершина v дерева T характеризуется тройкой параметров (P(v), t(v), M(v)). Точка P(v) уже была определена. Два других параметра вместе определяют прямую l(v), а именно t(v) определяет горизонтальность или вертикальность l(v); в первом случае l(v) – это прямая y = M(v) = y(P(v)), во втором случае – прямая x = M(v) = x(P(v)). Данный алгоритм накапливает выбираемые точки в списке U, первоначально пустом. Обозначая через D = [x1,x2]x[y1,y2] запросный регион, получаем, что поиск на дереве T осуществляется вызовом процедуры Search(корень(T), D).
Procedure Search(v,D);
Вход: v – вершина, D – регион.
Выход: внешний по отношению к процедуре список U точек.
begin
1
if ( t(v) = вертикаль) then [l,r] := [x1,
x2] else [l,r] := [y1, y2];
2
if (l £ M(v) £ r) then
3
if (P(v) Î D) then
4
U ¬ P(v);
5
if (v ¹ лист) then
6
if (l < M(v)) then Search(ЛевыйСын[v],D);
7
if (M(v) < r) then Search(ПравыйСын[v],D);
8
end
if;
end
proc.
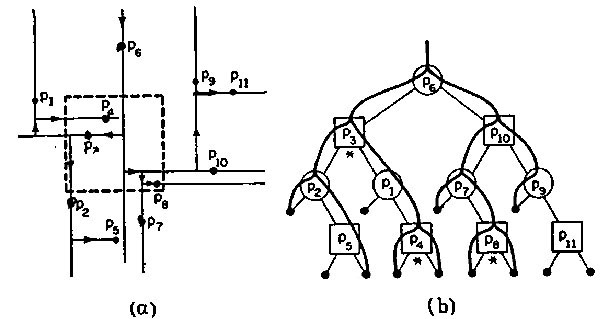
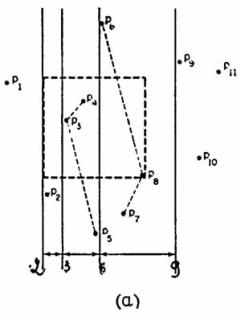
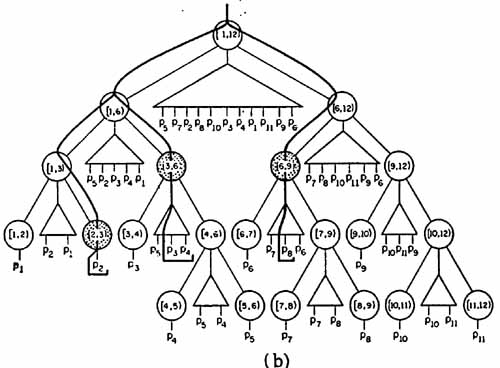
На рисунке показан пример регионального поиска. На рисунке (b) показан обход узлов T, осуществленный описанной выше процедурой поиска. Только в тех узлах, где поисковый обход раздваивается, производится проверка принадлежности точки региону. Звездочкой помечены те узлы, в которых такая проверка успешна, и соответствующая точка выбрана. Фактически выбранное множество – {p3, p4, p8}.
С точки зрения оценки сложности 2-D-дерево использует оптимальную память Q(N) (по узлу на точку из S). Кроме того, его можно построить за оптимальное время Q(N log N) следующим образом. Вертикальный разрез множества S производится в результате вычисления медианы множества x-координат точек из S за время O(|S|) (алгоритм из работы [Blum et al. (1973)]) и путем формирования разбиения S с такой же оценкой времени; аналогично и для горизонтального разреза. Итак за время O(N) исходное множество разбивается, в результате чего получаются полуплоскости, в каждой из которых по N/2 точек; тривиально получаем рекуррентное соотношение для времени T(N) работы алгоритма построения дерева: T(N) £ 2T(N/2) + O(N), что и дает оценку этого времени. В более прямой реализации этого построения обходятся без сложного алгоритма поиска медианы. Поскольку в только что описанном методе фактически производится сортировка множеств x- и y-координат путем рекурсивного поиска медианы, то мы можем прибегнуть к предварительной сортировке для формирования упорядоченных массивов абсцисс и ординат точек из S, именуемых соответственно x- и y-массивами. Это займет O(N log N) времени. Первый разрез производится выборкой (за константное время) медианы x-массива путем маркировки тех точек, чьи абсциссы, скажем, меньше этой медианы (за время O(N)). Маркировка позволяет быстро сформировать два отсортированных подмассива, и процесс для них рекуррентно повторяется.
Анализ времени запроса для худшего случая намного более сложен [Lee, Wong (1977)]. Очевидно, что время запроса пропорционально общему числу узлов в T, посещаемых поисковым алгоритмом, поскольку в каждом узле этот алгоритм затрачивает константное время. Очевидно, что это время потрачено в узле v не зря, если точка P(v) выбирается (продуктивный узел); иначе, этот узел считается непродуктивным. Анализ, проделанный Ли и Вонгом, направлен на построение ситуации худшего случая, т.е. он соответствует максимальному поддереву посещенных узлов, из которых все непродуктивны. Каждый узел v из T соответствует некоторому обобщенному прямоугольнику R(v). Пересечения запросного региона D и подобного обобщенного прямоугольника R(v) могут быть отнесены к разным типам в зависимости от числа сторон R(v), имеющих непустые пересечения с D. В частности, если обозначить это число через i, то говорят, что пересечение имеет тип i для i = 0, 1, 2, 3, 4.
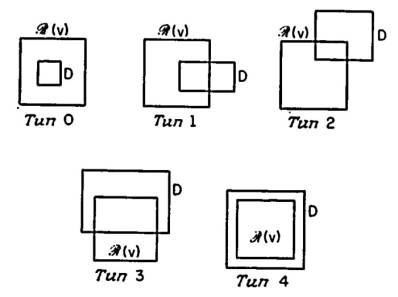
Единственный тип пересечений, который всегда продуктивен – это тип 4; все остальные могут оказаться непродуктивными. Ограничимся частными случаями пересечений типа 2 и 3. (Они могут начать появляться только на узлах, удаленных от корня на два и три уровня соответственно.)
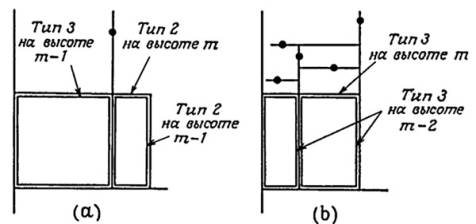
Рассматривая рисунок (a), можно легко построить ситуацию, когда пересечение типа 2 на высоте m непродуктивно и порождает одно пересечение типа 2 и одно пересечение типа 3 на высот (m – 1) (оба они могут быть сделаны непродуктивными). Аналогично, как показано на рисунке (b), при том же самом ограничении на типы непродуктивных узлов можно построить ситуацию, когда одно пересечение типа 3 на высоте m в T порождает пару пересечений типа 3 на высоте m-2. Итак, обозначая через Ui(m) число пройденных непродуктивных узлов в поддереве высотой m, чей корень имеет тип i (i =2, 3), получаем рекуррентные соотношения:
U2(m) = U2(m – 1) + U3(m
– 1) + 1,
U3(m) = 2 U3(m – 2) + 3.
Результат же таков: для U2(m) и U3(m)
получаем одинаковую оценку O(![]() ), следовательно, в худшем случае время запроса может
составить O(
), следовательно, в худшем случае время запроса может
составить O(![]() ) = O(
) = O(![]() ), даже если выбранное множество окажется пустым.
), даже если выбранное множество окажется пустым.
Оптимальные оценки по памяти и времени предобработки, к сожалению, не компенсируют обескураживающую оценку времени поиска для худшего случая. В качестве альтернативы предложены другие методы.
3 Метод прямого доступа и его варианты
Самый грубый способ минимизации времени поиска состоит в предварительном вычислении ответов на все возможные при региональном поиске запросы. Пусть дано множество S из N точек на плоскости, проведем горизонтальную и вертикальную прямые через каждую из этих точек. Эти прямые разобьют плоскость на (N + 1)2 прямоугольных ячеек. Положим, что в регионе D = [x1,x2]x[y1,y2] точка (x1,y1) принадлежит ячейке C1, а точка (x2,y2) – ячейке C2. Если теперь переместить как угодно любую из этих точек, оставляя её, однако, внутри соответствующей ячейки, то очевидно, что искомое множество (т.е. подмножество S, содержащееся внутри D) не изменится. Другими словами, пары ячеек формируют классы эквивалентности относительно результатов регионального поиска. Следовательно, число различных регионов, которые нам следовало бы рассмотреть, ограничено сверху числом
![]()
Если предварительно вычислить выбираемое множество для каждой из этих пар ячеек (затратив при этом O(N5) памяти), то мы получим схему, в которой поиск заканчивается после единственного обращения к файлу. Однако для достижения этой цели произвольный регион D нужно сопоставить паре ячеек, или, что то же самое, произвольная точка должна быть сопоставлена одной из ячеек. Очевидно, что это можно проделать двумя двоичными поисками на множестве абсцисс и ординат точек из S. На эту “нормализацию” уйдет O(log N) времени. Данный алгоритм слишком обременительный для практического использования из-за затрат памяти.
Заметим, что одномерный поиск является оптимальным по обеим мерам (времени поиска и памяти). Это замечание заставляет предположить возможность улучшения вышеописанного “метода ячеек”. В самом деле, можно объединить одномерный региональный поиск с локализацией региона методом прямого доступа [Bentley, Maurer (1982)]. Конкретно, для заданного региона D = [x1,x2]x[y1,y2] можно реализовать прямой доступ по координате x с последующим одномерным поиском по координате y. Для этого требуется, чтобы ко всем различимым упорядоченным парам абсцисс точек из S (x-регионы) был обеспечен прямой доступ; каждая такая пара (x’,x’’) в свою очередь связана с двоичным деревом поиска на ординатах точек, содержащихся в полосе x’ £ x £ x’’. Теперь удобно преобразовать исходную задачу, заменяя каждое действительное значение координаты её порядковым номером во множестве координат. Такое преобразование, именуемое нормализацией, осуществляется путем операции сортировки на каждом из множеств координат. После нормализации этих данных любой x-регион преобразуется за время O(N log N) в пару целых чисел (i, j) из отрезка [1,N+1] (i < j). Такая пара соответствует адресу в массиве указателей прямого доступа, который отсылает к двоичному дереву с (j - i) листьями. Поэтому общий объем памяти пропорционален
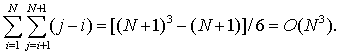
Заметим, что, хотя память удалось сократить с O(N5) до O(N3), время поиска осталось равным O(log N), поскольку и нормализация регионов, и одномерный региональный поиск используют O(log N) времени.
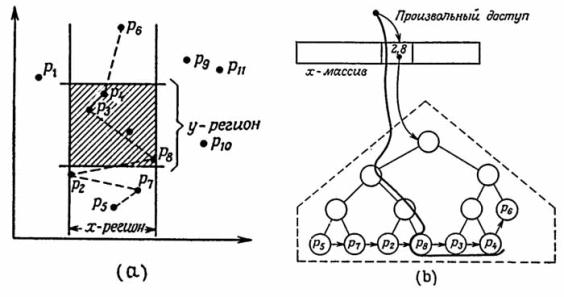
В массив x имеется доступ к региону [2, 8], заданному нормализованными абсциссам (рис. (b)); отсюда указатель направляет поиск к двоичному дереву. Там поиск, как таковой, заканчивается локализацией точки P8, после чего производится выборка последовательности (P8, P3, P4).
Очевидно,
что именно фаза прямого доступа в этой двухфазной схеме виновна в большой
затрате памяти. Поэтому улучшения нужно искать именно в этой фазе. Бентли и
Маурер предложили многоэтапный подход. Идея состоит в том, чтобы
последовательно использовать грубую сетку и мелкую сетку.
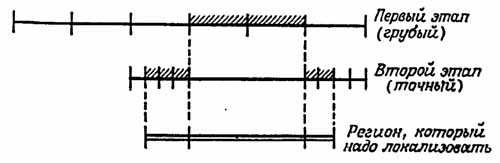
Все координаты нормализуются, и грубая сетка состоит из отрезков длиной k, при этом на каждом таком отрезке существует мелкая сетка, состоящая из отрезков единичной длины. Отсюда видно, что произвольный регион разбивается не более чем на три части, одна из которых целиком принадлежит грубой сетке, а две других – мелкой сетке. Каждой сетке соответствует описанный выше массив указателей прямого доступа. В частности, если грубая сетка состоит из Na шагов (0 < a £ 1), то на грубой сетке всего будет O(N2a) отрезков, а для соответствующей структуры данных потребуется O(N2a)xN = O(N1+2a) памяти. Аналогично каждая мелкая сетка состоит из N1-a шагов и всего будет Na таких сеток, поэтому общая память для них составит величину порядка Na x N(1-a)2 x N(1-a) = N3-2a. Минимального значения, равного O(N2), память достигает при a=1/2 без потери логарифмической оценки для времени регионального поиска. Мы получаем алгоритм, работающий за время O(log N) использующий O(N2) памяти. Обобщая этот подход, используя последовательность из l сеток возрастающей мелкости, для дальнейшего сокращения памяти при сохранении, однако, оценки времени поиска в пределах O(l log N). Таким образом приходим к следующему выводу:
Утверждение. Для любого e такого, что 0 < e < 1, региональный поиск на двумерном N-точечном файле можно провести с помощью алгоритма, использующего O(N1+e) памяти за время O(log N), основанного на многоэтапном методе прямого доступа.
4 Метод дерева регионов
Эффективность по времени поиска в методе прямого доступа получена благодаря построению набора “стандартных” отрезков. Выигрыш в памяти при переходе от одноэтапной схемы к двухэтапной получен благодаря сильному сокращению числа таких стандартных отрезков. Возникает стремление к дальнейшему следованию этой линии, т.е. к созданию схемы, минимизирующей число стандартных отрезков. В этом и состоит главная идея регионального дерева.
Рассмотрим множество на оси x, состоящее из N абсцисс, нормализованных до целых чисел из интервала [1,N] по их величине. Эти N абсцисс определяют N – 1 элементарных отрезков [i, i+1] для i = 1, 2, …, N – 1. Средством, которое будет использовано для реализации разбиения произвольного отрезка [i, j], является дерево отрезков.
Дерево отрезков, впервые введенное Дж. Бентли, это структура данных, созданная для работы с такими интервалами на числовой оси, концы которых принадлежат фиксированному множеству из N абсцисс. Поскольку множество абсцисс фиксировано, то дерево отрезков представляет собой статическую структуру по отношению к этим абсциссам, т.е. структуру, на которой не разрешены вставки и удаления абсцисс; кроме того, эти абсциссы можно нормализовать, заменяя каждую из них её порядковым номером при обходе их слева направо. Не теряя общности можно считать эти абсциссы целыми числами в интервале [1, N].
Дерево отрезков – это двоичное дерево с корнем. Для заданных целых чисел l и r таких, что l < r, дерево отрезков T(l,r) строится рекурсивно следующим образом: оно состоит из корня v с параметрами B[v] = l и E[v] = r (B и E мнемонически соответствуют словам “beginning” и “end”), а если r – l > 1, то оно состоит из левого поддерева T(l, ë(B[v] + E[v])/2û) и правого поддерева T(ë(B[v] + E[v])/2û, r). (Корни этих поддеревьев естественно обозначить через Lson[v] и Rson[v] соответственно.) Параметры B[v] и E[v] обозначают интервал [B[v], E[v] ] Í [l,r], связанный с узлом v. Интервалы, принадлежащие множеству {[B[v], E[v]]: v – узел T(l,r)}, называются стандартными интервалами дерева T(l,r). Стандартные интервалы, принадлежащие листьям T(l,r), называются элементарными интервалами (строго говоря, полуоткрытые интервалы [B[v], E[v]), за исключением самого правого пути в T(l,r), чьи интервалы замкнуты). Можно непосредственно убедиться, что T(l,r) сбалансировано (все его листья принадлежат двум смежным уровням) и имеет глубину élog2(r – l)ù.
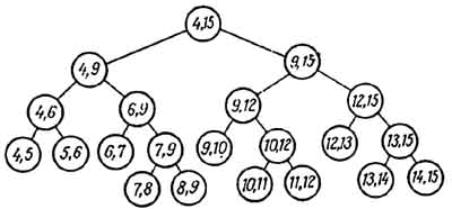
Произвольный отрезок, концы которого принадлежат множеству из N заданных абсцисс, может быть разбит деревом отрезков T(1,N) на не более 2*élog2Nù – 2 стандартных отрезков. Каждый стандартный отрезок отнесен к одному из узлов T(1, N), а те узлы, которые определяют разбиение отрезка [i, j], называются узлами отнесения для [i, j].
Дерево отрезков T(1, N) используется при поиске по x-координате. Этот поиск определяет уникальное множество узлов (узлов отнесения). Каждый такой узел v соответствует множеству из (E[v] – B[v]) абсцисс, т.е. множеству из (E[v] – B[v]) точек на плоскости. Ординаты этих точек образуют обычное прошитое двоичное дерево для регионального поиска в y-направлении. В результате построена новая структура данных, именуемая деревом регионов; его первичной структурой является дерево отрезков, заданных на абсциссах точек исходного множества S. В каждом узле этого дерева имеется указатель на прошитое двоичное дерево поиска (вторичные структуры).
Обобщение на d измерений можно провести весьма естественно. Пусть в d-мерном пространстве с координатными осями x1, x2, …, xd задано множество S из N точек. Эти координаты будут обрабатываться в следующем порядке: сначала x1, затем x2 и т.д. Предположим также, что все значения координат нормализованы. Дерево регионов строится рекурсивно следующим образом:
(1) Первичное дерево отрезков T* соответствует множеству {x1(p): p Î S}. Для каждого узла v из T* обозначим через Sd(v) – множество точек из S, проецирующихся на отрезок [B[v], E[v]] по координате x1. Определим (d – 1) -мерное множество:
Sd-1(v) D {(x2(p), …, xd(p)): p Î S}.
(2) Узел v из T* имеет указатель на дерево регионов для Sd-1(v).
Дерево отрезков можно считать не только инструментом для разбиения любого отрезка на логарифмическое число кусков, но также и способом применения метода “разделяй и властвуй” к региональному поиску.
Заметим, что во-первых при d ³ 2 каждый узел отнесения из проекции запросного региона на ось x1 (их всего O(log N)) порождает отдельную (d – 1)-мерную задачу регионального поиска. В частности, узел v порождает поиск на n(v) D E[v] – B[v] точках. Обозначая через Q(N, d) время поиска для файла из N штук d-мерных точек, получаем простое рекуррентное соотношение:
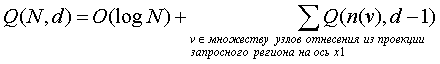
Первый член в правой части этого уравнения появился из-за поиска на первичном дереве отрезков, а второй член объясняется наличием (d – 1)-мерных подзадач. Поскольку существует не более 2*élog2Nù – 2 узлов отнесения и n(v) £ N (очевидно), то получаем
Q(N, d) = O(log N)Q(N, d – 1)
Поскольку Q(N, 1) = O(log N) для двоичного поиска, то получаем оценку времени поиска:
Q(N, d) = O((log N)d).
Обозначая через S(N, d) память, занятую деревом регионов, получаем рекуррентное соотношение
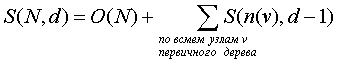
где первый член в правой части соответствует памяти, занятой первичным деревом, а второй член соответствует всем (d – 1)-мерным деревьям. Оценка второго члена очень проста, если N есть степень 2; в противном случае будет использована столь же эффективная простая аппроксимация. Существует не более двух узлов v с n(v) = 2élog2Nù – 1, не более четырех – с n(v) = 2élog2Nù – 2 и т.д. Поэтому эту сумму можно оценить сверху следующим образом:
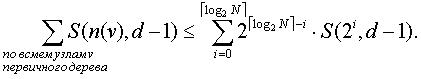
Учитывая эту аппроксимацию и замечая, что S(N, 1) = O(N) – память под прошитое двоичное дерево, получаем решение
S(N, d) = O(N logd-1N).
Для оценки времени предварительной обработки можно следовать той же самой схеме рассуждений. Итог можно подвести в следующем выводе.
Утверждение. Региональный поиск на d-мерном файле из N точек можно провести за время O(logd N) используя O(N logd–1N) памяти, затратив O(N logd–1N) на предобработку. Алгоритм основан на методе дерева регионов.
В частности, при d = 2 эти меры – время
запроса, память и время предварительной обработки выглядят так: O(log2 N + k), O(N log N) и
O(N log N) соответственно.