Скачать в формате DOC (архив RAR)
Отыскание неподвижных точек
методом Ньютона.
Источники:
1)
“Неподвижные точки точечного отображения плоскости в плоскость” методическая
разработка; составители: З.С. Баталова, канд. физ.-мат. наук, Н.А.
Ежевская, канд. физ.-мат. наук.
ННГУ
1991.
2)
“Алгоритмы и программы численного исследования динамических систем” учебное
пособие; составители: Ю.И. Неймарк, З.С. Баталова и др.
ННГУ
(ГГУ) 1983.
При изучении динамических систем, описываемых обыкновенными
дифференциальными уравнениями, возникает задача отыскания и исследования
стационарных и периодических движений. Эта задача может быть сведена к
нахождению неподвижных точек точечного отображения некоторой секущей
поверхности в себя, порождаемого фазовыми траекториями динамической системы.
При этом тип неподвижной точки отображения (устойчивая, неустойчивая, седловая)
совпадает с типом соответствующего ей
стационарного или периодического движения.
Рассмотрим нелинейную автономную систему:
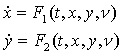(1)
где F – дифференцируемые функции переменных x и y,
непрерывные периодические функции по t с периодом 
, 
- параметр. Задача исследования системы сводится к построению
и изучению точечного отображения секущей плоскости t=0 в себя.
Обозначим через T оператор точечного
отображения секущей плоскости в себя.
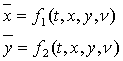(2)
– его неподвижная точка: T(
) = 
.
Представим соотношение (2) в виде
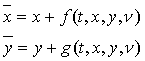(3)
Тогда задача поиска неподвижной точки сведется к решению системы двух
уравнений:
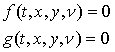(4)
Для решения этой системы применим метод последовательных приближений
(метод Ньютона). Примем значение параметра постоянным.
Пусть 
является k-ым
приближением неподвижной точки. Разложим Функции 
и 
в ряд Тейлора в
окрестности точки 
:
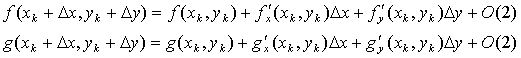(5)
Предполагаем, что переход от 
к 
приближает значение
функций f и g к нулю так, что
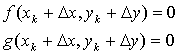(6)
Отбрасывая в (5) квадратичные члены, получим систему
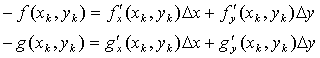(7)
которая является линейной алгебраической системой уравнений
относительно 
и 
. По правилу Крамера её решение запишется в виде:
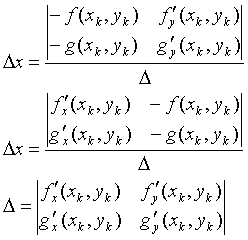(7)
Тогда k+1 приближение неподвижной точки определяется
формулами:
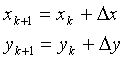(8)
Итерационный процесс заканчивается, если выполнено условие
(9)
где 
- малое положительное
число.
Для применения метода Ньютона необходимо определить значения функций f и g. Однако, в силу
нелинейности и неавтономности системы эти функции не могут быть найдены в
аналитическом виде. Для их отыскания применим следующий способ.
Пусть 
– решение системы (1), удовлетворяющее начальным
условиям 
, полагая 
, получим точку 
, где
(10)
Отсюда найдем значения f и g в
виде разностей
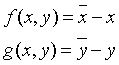(11)
Продифференцируем эти выражения по x и y,
получим
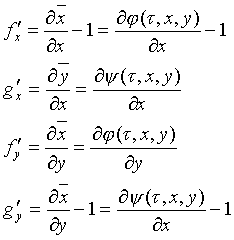(12)
Поскольку 
– решение системы (1), то справедливы тождества
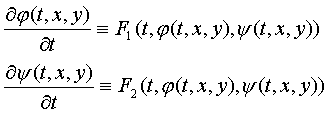(13)
Продифференцируем (13) по x и y :
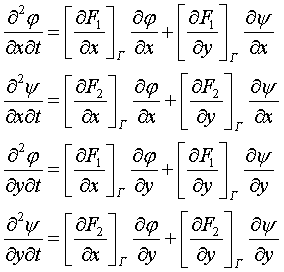(14)
где частные производные функций 
и 
вычисляются при тех
же значениях аргументов, что и в (13). Правые части соотношений (14) непрерывны
по предположению, поэтому можно изменить порядок дифференцирования смешанных
производных.
Обозначим
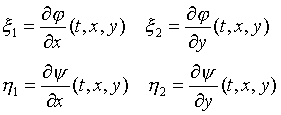(15)
Тогда соотношения (14) запишутся в виде системы
(16)
При 
справедливы
соотношения 
. Дифференцируя эти равенства по x и y, получим начальные условия
для решения системы (16).
(17)
Таким образом, для вычисления значений 
в точке M(x,y), необходимо найти решение
системы (16) при 
и подставить их в формулы
(12).
Таким образом для отыскания неподвижных точек
отображения T на k-ом шаге необходимо
интегрировать объединение систем (1) и (16) с начальными условиями 
и (17) на интервале 
.
Решение системы (1), (16) может быть найдено
лишь численно, причем в системе (16) коэффициенты являются функциями переменных
.
Для определения характера устойчивости
найденной неподвижной точки 
необходимо построить характеристический полином,
соответствующий этой точке. С этой
целью находится решение системы (1), (16), удовлетворяющее начальным условиям
Характеристическое уравнение имеет вид
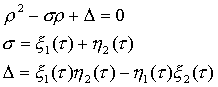
Корни этого уравнения определяют тип неподвижной точки 
.
Если они лежат внутри круга единичного радиуса, то 
является асимптотически устойчивой в малом. Если оба корня
расположены вне круга, то точка неустойчива. Если корни действительны и 
, то точка имеет седловой тип. Случай, когда один из них или
оба лежат на границе круга является бифуркационным.
Скачать
в формате DOC (архив RAR)
