Метод Рунге-Кутта пятого порядка, модификация Мерсона.

Требуется интегрировать систему вида

(x является вектором).

Существует целое семейство методов Рунге-Кутта. Погрешность на шаге интегрирования метода n-ого порядка равна , k – некоторая постоянная, h – шаг интегрирования. Чтобы оценить ошибку необходимо определить верхние пределы для k. Оказывается, это не простая задача. А без знания ошибки на шаге трудно правильно выбрать величину шага. Это является одним из недостатков методов Рунге-Кутта с постоянным шагом. В методах с автоматическим выбором шага есть критерий, указывающий на необходимость изменения шага.

Одним из таких методов является метод Мерсона. Расчетные формулы имеют вид:

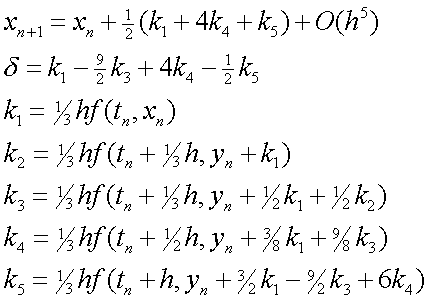
– погрешность на шаге.

Предлагается следующий критерий изменения шага интегрирования h: если ошибка на шаге в пять раз превосходит предписанную погрешность , то вычисления снова повторяются от прежней точки с уменьшенным вдвое шагом h/2. При выполнении неравенства , интегрирование продолжается от новой точки с удвоенным шагом. Если , то шаг не меняется.

Скачать в формате DOC (архив RAR)

<< на главную